DES 算法

Web Security Homework1

1. 算法原理概述

1.1 算法原理图

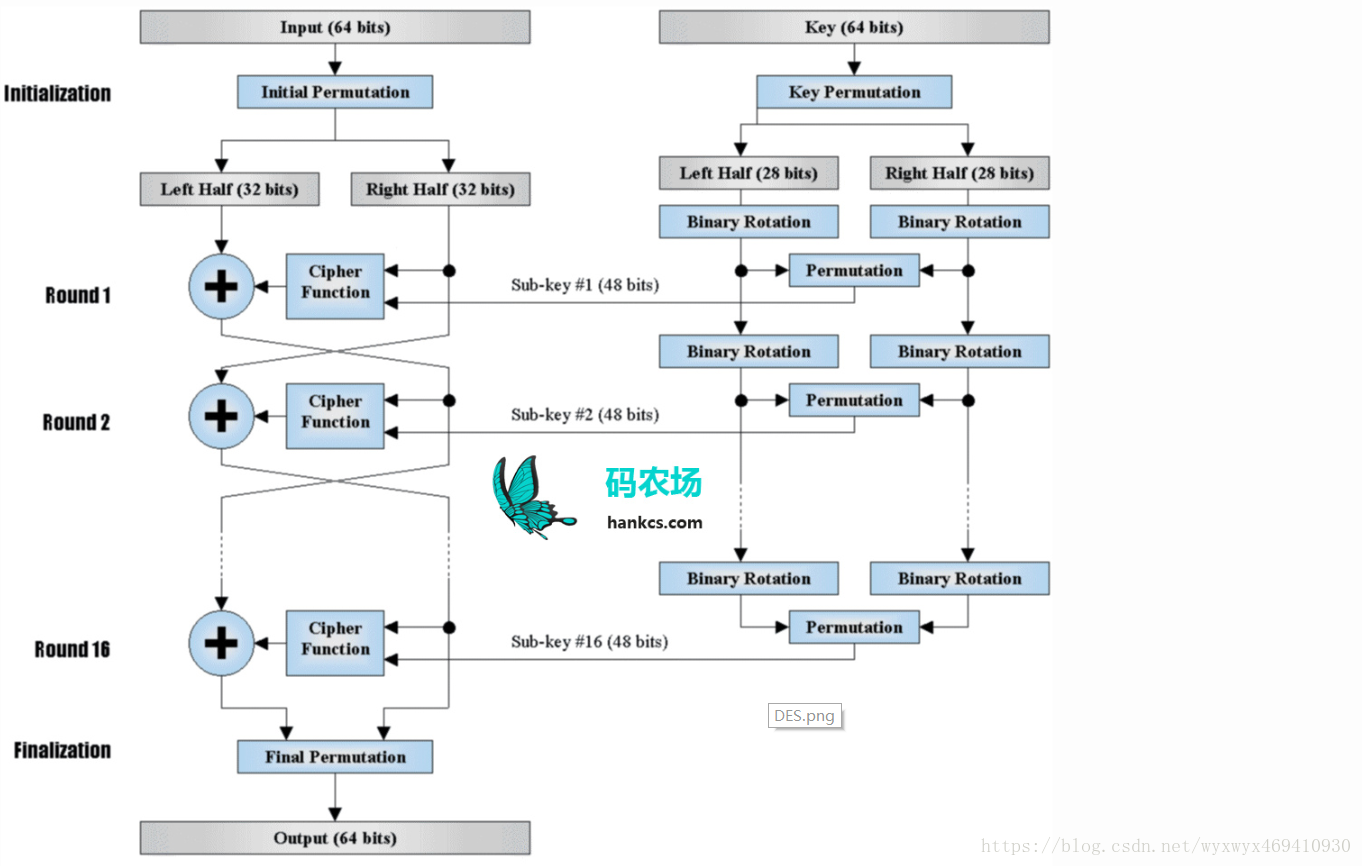
1.2 自然语言描述

1.2.1 加密过程

输入16位16进制明文M -> 将M分为L(32位)R(32位) ->

创建16个48位长的子秘钥 -> 创建S盒 ->

创建加密函数 -> 使用加密函数加密明文M得到新序列L’R’ ->

拼接L‘R‘ -> 输出加密序列16位16进制加密序列M‘

1.2.2 解密过程

解密的运行过程与加密的运行过程只有在进行16轮迭代时候有差异，其余过程相同。

2. 总体结构

des.h ：整个程序的主体
data_table.h ：包含S盒与PC表格
function.h ：各种功能函数，包括
- Test函数：检测输入的明文是否是16位16进制数据，若大于16位，则只取前16位；若小于16位，则末尾补0
- HexToBi函数：转16进制数据为2进制数据
- BiToHex函数：转2进制数据为16进制数据
- HexPrint函数：输出十六进制数据
- Binary函数：输出二进制数据
- LeftShift函数：向左移位
- Reverse函数：反转数据
- GenerateSubKeys：64位秘钥产生48位子秘钥

3. 模块分解

3.1 输入检测模块

在此模块中，我们先对需要进行加密的明文和要用到的密文序列进行检测：

若出现非十六进制数据，则将该位置上的数据更改为0
若序列长度大于16位，则只取前16位数据
若序列长度小于16位，则在数据末尾补0，直到序列长度满足16位

代码：

//异常处理
for(int i = 0 ; i < test.size() ; i ++ )
{
    if( ( '0' <= test[i] && test[i] <= '9' )  || ( 'A' <= test[i] && test[i] <= 'F' ) || ( 'a' <= test[i] && test[i] <= 'f' ) )
    {
        continue ;
    }
    else
    {
        test[i] = '0' ;
    }
}
//检查字符串长度
int Charnumber = test.size() ;
int Processamount = Charnumber / 16 ;
int Blankamount = Charnumber % 16 ; 
if( Blankamount != 0 )
{
    if( Processamount == 0 )
    {
        for(int i = Blankamount ; i < 16 ; i++ )
            test = test + '0' ;
    }
    else
        test.erase(16) ;
    ｝
｝

3.2 数据划分模块

DES是一个基于组块的加密算法，这意味着无论输入还是输出都是64位长度的。也就是说DES产生了一种最多264种的变换方法。每个64位的区块被分为2个32位的部分，左半部分L和右半部分R。（这种分割只在特定的操作中进行。）

比如，取明文M为

M = 0123456789ABCDEF

这里的M是16进制的，将M写成二进制，我们得到一个64位的区块：

M = 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
L = 0000 0001 0010 0011 0100 0101 0110 0111
R = 1000 1001 1010 1011 1100 1101 1110 1111

M的第一位是0，最后一位是1，我们从左读到右。

DES使用56位的秘钥操作这个64位的区块。秘钥实际上也是储存为64位的，但每8位都没有被用上（也就是第8, 16, 24, 32, 40, 48, 56, 和64位都没有被用上）。但是，我们仍然在接下来的运算中将秘钥标记为从1到64位的64个比特。不过，你也许会看到，刚刚提到的这8个在创建子秘钥的时候会被忽略掉。

举个例子，取十六进制秘钥K为

K = 133457799BBCDFF1

我们可以得到它的二进制形式（1为0001，3为0011.依次类推，并且将每八位写成一组。这样每组的最后一位都没有被用上。）

K = 00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001

代码：

char *L = new char[33] ; L[32] = '\0';
char *R = new char[33] ; R[32] = '\0';
for(int i = 0; i < 32; i++)
{
    L[i] = BiMsg[i] ; 
    R[i] = BiMsg[i + 32] ;
}

3.3 秘钥PC变换模块

从3.2中我们了解到，我们是使用输入的64位秘钥来对64位明文进行加密操作的，但是我们输入的64位秘钥并不能直接进行使用，首先需要对这64位秘钥进行一次 PC-1 变换，这里我们需要注意一点我们在变换后，原秘钥只会有 56 位保留下来，例如：

比如，对于原秘钥：

K = 00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001

我们将得到56位的新秘钥：

K’ = 1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111

然后，将这个秘钥拆分为左右两部分，C0 和 D0，每半边都有28位。

比如，对于新秘钥，我们得到：

C0 = 1111000 0110011 0010101 0101111
D0 = 0101010 1011001 1001111 0001111

代码：

//PC-1置换
for(int i = 0; i < 56; i++)
{
    int index = PC1Table[i] - 1 ; 
    realKey[i] = BiKey[index] ;
}

//C和D
char *C = new char[29] ; 
C[28] = '\0' ;
char *D = new char[29] ; 
D[28] = '\0' ;
for(int i = 0; i < 28; i++)
{
    C[i] = realKey[i] ;
}
for(int i = 0, j = 28; i < 28; i++, j++)
{
    D[i] = realKey[j];
}

3.4 生成16个子秘钥模块

拿到3.3生成的 C0 和 D0后,我们需要对其进行移位操作，进而得到16个块 Cn 和 Dn (1<=n<=16)（注：每一对Cn 和 Dn都是由前一对Cn-1 和 Dn-1移位而来）

具体说来，对于n = 1, 2, …, 16，在前一轮移位的结果上，使用下表进行一些次数的左移操作。

1
2
3

static int LeftShiftTable[16]={
	 1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1
};

在完成左移之后，我们对得到的 16 对Cn和Dn进行PC-2变换，变换前 CnDn是56位的，但是进行 PC-2变换之后，原先的 56 位数据就只剩下了 48 位，举例：

比如，对于第1轮的组合秘钥，我们有：

C1D1 = 1110000 1100110 0101010 1011111 1010101 0110011 0011110 0011110

通过PC-2的变换后，得到：

K1 = 000110 110000 001011 101111 111111 000111 000001 110010

其他各段数据变换规则同上。

代码：

for(int k = 0; k < 16; k++)
{
    //左移
    LeftShift(C, LeftShiftTable[k]) ;
    LeftShift(D, LeftShiftTable[k]) ;
    char * CDCombine = new char[57] ;  CDCombine[56] = '\0';
    for(int i = 0; i < 28; i++)
    {
        CDCombine[i] = C[i] ;
        CDCombine[i+28] = D[i] ;
    }
    //PC-2置换
    for(int i = 0; i < 48; i++)
    {
        int index  = PC2Table[i] - 1 ; 
        subKey[k][i] = CDCombine[index] ; 
    }
    subKey[k][48] = '\0';
}

3.5 明文数据变换模块

在处理完秘钥之后，我们需要对输入的明文M进行IP变换，IP变换是按照按照 IP表进行：

char * BiMsgCopy = new char[65] ;
memcpy(BiMsgCopy, BiMsg, 65 * sizeof(char));
for(int i = 0; i < 64; i++)
{
    int index  = IPTable[i] - 1 ; 
    BiMsg[i] = BiMsgCopy[index] ; 
}

比如：

比如，对M的区块执行初始变换，得到：

M = 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

变换后：

IP = 1100 1100 0000 0000 1100 1100 1111 1111 1111 0000 1010 1010 1111 0000 1010 1010

3.6 IP序列加密模块

在3.5中我们得到变换后的序列 IP ，将 IP 序列分为左半边L0 和32位的右半边R0 。

比如，对于上例，我们得到：

L0 = 1100 1100 0000 0000 1100 1100 1111 1111
R0 = 1111 0000 1010 1010 1111 0000 1010 1010

我们接着执行16个迭代，对1<=n<=16，使用一个函数f。函数f输入两个区块——一个32位的数据区块和一个48位的秘钥区块Kn ，最终输出一个 32 位的区块。我们最终就有如下计算规则：

Ln = Rn-1
Rn = Ln-1 XOR f(Rn-1,Kn)

这样我们就得到最终区块，也就是n = 16 的 L16R16。这个过程从本质上理解就是，我们拿前一个迭代的结果的右边32位作为当前迭代的左边 32 位。对于当前迭代的右边 32 位，将它和上一个迭代的f函数的输出执行XOR运算。

比如，对n = 1，我们有：

K1 = 000110 110000 001011 101111 111111 000111 000001 110010
L1 = R0 = 1111 0000 1010 1010 1111 0000 1010 1010
- R1 = L0 + f(R0,K1)

我们在进行 16 次操作之后，便得到L16R16 序列，再对R16L16进行一次IP逆变换也即得到我们所要求的加密序列M‘。

比如：

我们得到了第16轮的左右两个区块：

L16 = 0100 0011 0100 0010 0011 0010 0011 0100
R16 = 0000 1010 0100 1100 1101 1001 1001 0101

我们将这两个区块调换位置，然后执行最终变换：

R16L16 = 00001010 01001100 11011001 10010101 01000011 01000010 00110010 00110100
M‘ = IP-1 = 10000101 11101000 00010011 01010100 00001111 00001010 10110100 00000101

代码：

//异或
for(int i = 0; i < 48; i++)
{
    char * temp = new char[65]; 
    if(mode == 0) 
    {
        memcpy(temp, subKey[k], 48);
    }
    else if(mode == 1) 
    {
        memcpy(temp, subKey[15 - k], 48); 
    }
    if(ExtendedR[i] == temp[i])
    {
        ExtendedR[i] = '0';
    }
    else
    {
        ExtendedR[i] = '1';
    }
}
//32位互换
char *RLChange = new char[65] ;
for(int i = 0 ; i < 32 ; i++)
{
    RLChange[i] = R[i] ;
    RLChange[i + 32] = L[i] ; 
}
//逆初始置换
char *Cipher = new char[65] ; 

Cipher[64] = '\0';
for(int i = 0; i < 64; i++)
{
    int index = RIPTable[i] - 1 ;
    Cipher[i] = RLChange[index] ;
}

3.7 f(R0,K1)函数模块

为了计算f(R0,K1)，我们首先拓展每个Rn-1，将其从32位拓展到48位。这个扩展过程实则是使用表E来重复Rn-1中的一些位来实现的。扩展Rn-1这一步通过使用函数E实现,也即函数E(Rn-1)输入32位输出48位数据。

定义E为函数E的输出，将其写成8组，每组6位。这些比特是通过选择输入的某些位来产生的，具体实现如下：

char * ExtendedR = new char[49] ; ExtendedR[48] = '\0';
for(int i = 0 ; i < 48 ; i++)
{
    int index = ExtendedETable[i] - 1 ; 
    ExtendedR[i] = R[index] ;
}

比如，给定R0 ，我们可以计算出E(R0) ：

R0 = 1111 0000 1010 1010 1111 0000 1010 1010
E(R0) = 011110 100001 010101 010101 011110 100001 010101 010101

（注意输入的每4位一个分组被拓展为输出的每6位一个分组。）

接着在f函数中，我们对输出E(Rn-1) 和秘钥Kn执行XOR运算：

Kn XOR E(Rn-1)

比如，对K1 , E(R0)，我们有：

K1 = 000110 110000 001011 101111 111111 000111 000001 110010
E(R0) = 011110 100001 010101 010101 011110 100001 010101 010101
K1+E(R0) = 011000 010001 011110 111010 100001 100110 010100 100111.

到这里我们还没有完成f(R0,K1)函数的运算，我们使用一张表E将Rn-1 从32位拓展为48位，并且对这个结果和秘钥Kn执行了异或运算。还要对每组的6比特执行一些奇怪的操作：我们将它作为一张被称为“S盒”的表格的地址。每组6比特都将给我们一个位于不同S盒中的地址。在那个地址里存放着一个4比特的数字。这个4比特的数字将会替换掉原来的6个比特。最终结果就是，8组6比特的数据被转换为8组4比特（一共32位）的数据。

将上一步的48位的结果写成如下形式：

Kn + E(Rn-1) = B1B2B3B4B5B6B7B8,

每个Bi 都是一个6比特的分组，我们现在计算

S1(B1) S2(B2) S3(B3) S4(B4) S5(B5) S6(B6) S7(B7) S8(B8)

注：Si(Bi) 指的是第i个S盒的输出，S盒的计算方式为：B的第一位和最后一位组合起来的二进制数决定一个介于0和3之间的十进制数（或者二进制00到11之间）。设这个数为i。B的中间 4 位二进制数代表一个介于 0 到 15 之间的十进制数（二进制0000到1111）。设这个数为j。查表找到第i行第j列的那个数，这是一个介于 0 和 15 之间的数，并且它是能由一个唯一的 4 位区块表示的。这个区块就是函数S1 输入B得到的输出S1(B) 。

比如：

对输入B = 011011 ，第一位是 0 ，最后一位是 1 ，决定了行号是 01 ，也就是十进制的 1 。中间 4 位是1101，也就是十进制的 13 ，所以列号是 13 。查表第 1 行第 13 列我们得到数字 5 。这决定了输出；5 是二进制0101，所以输出就是 0101 。也即S1(011011) = 0101。

第一轮变换之后，我们得到 8 个S盒的输出f = P(*S1(B1)S2(B2)…S8(B8)),变换 P 由表P决定，通过下标产生32位输出，那么：

R1 = L0 + f(R0 , K1 )
- = 1100 1100 0000 0000 1100 1100 1111 1111
- XOR 0010 0011 0100 1010 1010 1001 1011 1011
- = 1110 1111 0100 1010 0110 0101 0100 0100

在完成16次的 函数f 计算之后，就可以得到L16与R16序列，也即我们要求得的函数输出的最终结果，但是这并不是最终的加密序列，我们需要回到3.6，进行最后一步转置的变换操作。

// 部分代码
int target = SBox[s][x][y] ;  
char *biTarget = new char[5] ;
for(int i = 3, index = 0 ; i >= 0 ; i--, index++)
{  
    if(target & (1 << i))  
        biTarget[index] =  '1';  
    else  
        biTarget[index] =  '0';  
}
biTarget[4] = '\0' ;

for(int i = 0 ; i < 4 ; i++)
{
    R[indexR] = biTarget[i] ;
    indexR++ ;
}

4. 数据结构

4.1 输入的明文与密文序列

//创建待加密明文序列
char HexMsg[17] ; 
memset(HexMsg,0,sizeof(char)*17);
//创建密文序列
char HexKey[17] ;
memset(HexKey,0,sizeof(char)*17);

//测试输入序列
cout << "Input the pending sequence" << endl ;
cout << "Sequence:";
string Testinput ;
//输入铭文序列
cin >> Testinput ;
Testinput = Test(Testinput);

4.2 IP置换表与IP逆置换表

//IP置换表
int IP[64]={  
	//L部分
	58,50,42,34,26,18,10, 2,
	60,52,44,36,28,20,12, 4,
	62,54,46,38,30,22,14, 6,
	64,56,48,40,32,24,16, 8,
	//R部分
	57,49,41,33,25,17, 9, 1,
	59,51,43,35,27,19,11, 3,
	61,53,45,37,29,21,13, 5,
	63,55,47,39,31,23,15, 7 
};
//IP逆置换表
int ReverseIP[64]={              
	40, 8,48,16,56,24,64,32,
	39, 7,47,15,55,23,63,31,
	38, 6,46,14,54,22,62,30,
	37, 5,45,13,53,21,61,29,
	36, 4,44,12,52,20,60,28,
	35, 3,43,11,51,19,59,27,
	34, 2,42,10,50,18,58,26,
	33, 1,41, 9,49,17,57,25	
};

4.3 S盒

int SBox[8][4][16]={
	//S1
	14, 4,13, 1, 2,15,11, 8, 3,10, 6,12, 5, 9, 0, 7,
	 0,15, 7, 4,14, 2,13, 1,10, 6,12,11, 9, 5, 3, 8,
	 4, 1,14, 8,13, 6, 2,11,15,12, 9, 7, 3,10, 5, 0,
	15,12, 8, 2, 4, 9, 1, 7, 5,11, 3,14,10, 0, 6,13,
...

5. 运行结果

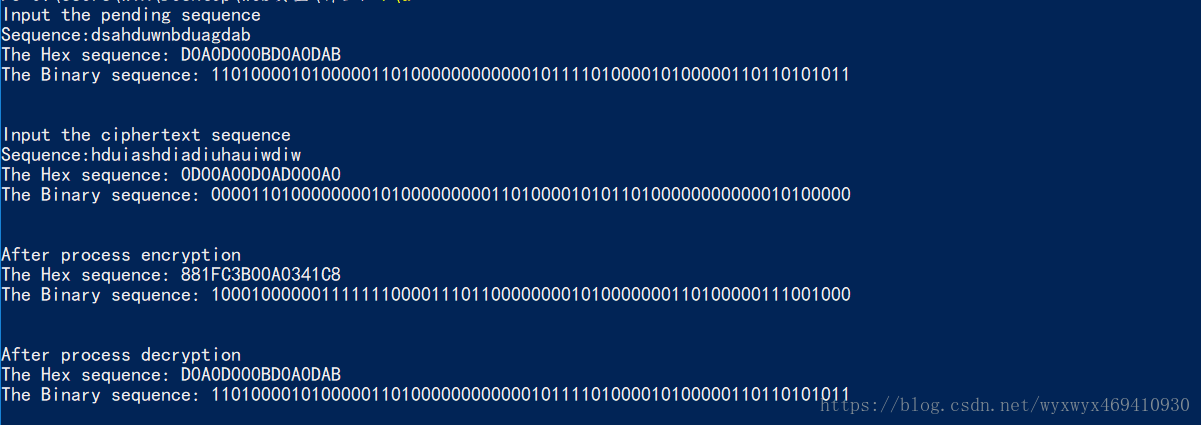
注：

Pengding sequence：明文序列
Ciphertext sequence：秘钥序列
encryption ：加密后
decryption ：解密后

通过解密后得到最初未加密明文可知，我们的加密过程是正确的。

6. 程序代码

我的github以及打包附件中

7. 参考文献

DES算法详解
蔡老师的PPT